Diffusion Transformers(DiT) from Scratch
Skip to a section
Background
In this file, I implemented Diffusion Transformers from scratch. Here is the GitHub link but I'd love for you to read on. I also trained them with moderate success which I’d put down to being limited with GPU compute/data processing money(was limited to spending a sum total of $80) - nonetheless it was a lot of fun to do.
Before I break down DiTs, I want to explain the incumbent method that is used to perform diffusion - DDPMs. DDPMs are generative models that learn to generate data by iteratively denoising samples. The process begins by iteratively adding noise to a clean image through a series of timesteps where noise being added is sampled from a Gaussian distribution, thereby turning the image into a Gaussian distribution after processing through said timesteps. The forward process is denoted by q(xt∣xt−1 )=N(xt;1−βt xt−1 ,βt I) where βt is the noise variance at timestep t. Noise variance (βt) acts as a hyperparameter that controls the intensity of noise added at each step. Think of it like photocopying an image repeatedly, but each time you add a tiny bit of smudge to the copy. After enough copies, the image becomes so blurry that it looks like static noise. The goal of DDPMs is to learn how to reverse this process—starting from the noisy image and carefully removing the smudges step by step to recover the original image.
The forward process is mathematically expressed as:
q(xt∣xt−1 ) = N(xt, (sqrt(1 - βt) * xt−1), βt * I)
Here:
- xt represents the image (or data) at timestep t
- xt-1 is the image at the previous timestep t-1
- βt is the noise variance at timestep t
- I is the identity matrix, representing isotropic Gaussian noise
As this process unfolds over multiple timesteps, the image progressively loses its structure and approaches a Gaussian distribution.
To express the overall forward process starting from the original data, the formulation becomes:
q(xt|x0) = N(xt; ᾱt x0, (1-ᾱt) I) where ᾱt denotes the cumulative product of (1 - βt) terms across timesteps.
Once the data is sufficiently corrupted, the reverse process aims to progressively remove the noise, reconstructing the original data. By training a neural network typically based on a U-Net architecture to predict and remove this noise, DDPMs can generate high-fidelity samples by reversing the diffusion process step by step.
The U-Net architecture, named for its U-shaped structure, consists of:
- Encoder Path (Contracting): A series of convolutional and max pooling layers that progressively reduce spatial dimensions while increasing the number of channels. This helps capture hierarchical features and context.
- Bottleneck: The deepest part of the network where the spatial dimensions are smallest but feature channels are highest.
- Decoder Path (Expanding): A series of upsampling and convolutional layers that gradually restore spatial dimensions while decreasing channels.
- Skip Connections: Direct connections between corresponding encoder and decoder layers that help preserve fine-grained details that might otherwise be lost during downsampling.
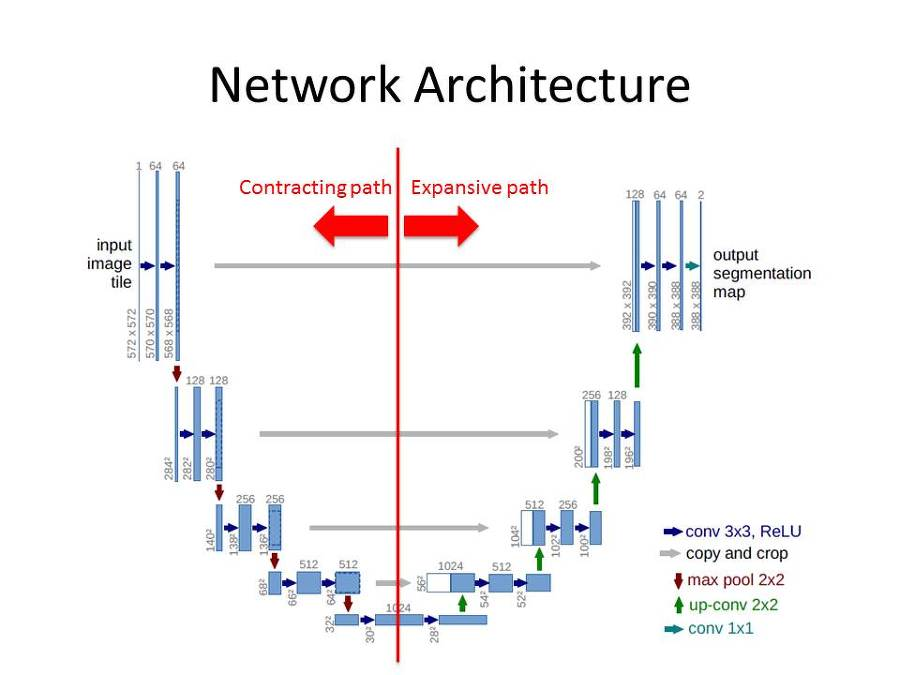
U-Nets rely heavily on convolutional downsampling, upsampling, and skip connections, making the architecture relatively rigid, expensive and challenging to modify. Not a lot of changes can be made to the core architecture.
Transformers, in contrast, offer greater flexibility and scalability. Key advantages of transformers include:
- Modularity: Transformers can incorporate various attention mechanisms (self-attention, cross-attention) and normalization techniques.
- Scalability: Transformers scale effectively to billions of parameters, aligning with the scaling laws of data and compute.
- Generalization: The architecture is not inherently tied to a particular input modality, allowing easy adaptation to diverse tasks.
Diffusion Transformers(DiTs) are a new class of diffusion models based on the transformer architecture that replace the commonly used U-Net architecture with transformers to create high resolution images. In most cases, the model directly outputs denoised images rather than removing noise every step(like U-Nets) which are compared to the original image aiding in training DiT model. Now, let’s dive into how this looks:
Most diffusion models, transformer and U-Net based, work in the latent space where pre-processed or processed n x n sized images are decomposed to a k-dimensional space latent where k < n. This makes it less computationally expensive to run the model on a smaller distribution space than pixel space. Prior to encoding these images, they’re preprocessed in the order that they’re scaled to 256 x 256 maintaining the aspect ratio and center cropping the image. The smallest side is scaled to 256 first, ensuring consistency across images, a technique rooted in early computer vision pipelines where handling variable-sized images was computationally expensive and models performed better with uniform input sizes. The images are then horizontally flipped with a certain probability and normalised to values between -1 and 1. Both are long-standing methods that enhance model convergence and accuracy by reducing variance in input data.
def center_crop_arr(pil_image, image_size):
# Downsample large images to prevent excessive memory usage
# If image is more than 2x target size in both dimensions, reduce by half until it's not
while min(*pil_image.size) >= 2 * image_size:
pil_image = pil_image.resize(
tuple(x // 2 for x in pil_image.size), resample=Image.BOX
)
# Calculate scale factor to resize the smallest dimension to target size
# This maintains aspect ratio while ensuring image is large enough
scale = image_size / min(*pil_image.size)
pil_image = pil_image.resize(
tuple(round(x * scale) for x in pil_image.size), resample=Image.BICUBIC
)
# Convert to numpy array for center cropping
arr = np.array(pil_image)
# Calculate crop coordinates to take center portion
crop_y = (arr.shape[0] - image_size) // 2
crop_x = (arr.shape[1] - image_size) // 2
# Return center-cropped image of exact target size
return Image.fromarray(arr[crop_y: crop_y + image_size, crop_x: crop_x + image_size])
def preprocess_image(image, target_size=256):
# Create a transformation pipeline using torchvision.transforms
transform = T.Compose([
# Step 1: Center crop the image to target size while maintaining aspect ratio
T.Lambda(lambda pil_image: center_crop_arr(pil_image, target_size)),
# Step 2: Randomly flip image horizontally for data augmentation
T.RandomHorizontalFlip(),
# Step 3: Convert PIL image to tensor (changes to range [0, 1])
T.ToTensor(),
# Step 4: Normalize pixel values to range [-1, 1] using mean and std of 0.5
T.Normalize(mean=[0.5, 0.5, 0.5], std=[0.5, 0.5, 0.5])
])
# Apply the transformation pipeline
image_tensor = transform(image)
# Verify the output dimensions are correct
if image_tensor.shape[1:] != (target_size, target_size):
raise ValueError(f"Image tensor size mismatch: expected ({target_size}, {target_size}), got {image_tensor.shape[1:]}")
return image_tensor
For the encoding procedure, I used an auto-encoder from the diffusers library by the name of madebyollin/sdxl-vae-fp16-fix and a corresponding text encoder from the sentence-transformers library called sentence-transformers/clip-ViT-L-14. This model is optimised for handling text tokens greater than 784 tokens, a restriction for several text encoders. I will come to why we need an encoder to support greater than 784 tokens soon.
def encode_latent(vae, image):
with torch.no_grad():
latent = vae.encode(image.unsqueeze(0).to(vae.device)) # Add batch dimension
return latent.latent_dist.sample().squeeze(0).cpu() # don’t use the mean - use the .sample
def load_clip_text_encoder(model_name="sentence-transformers/clip-ViT-L-14"):
return SentenceTransformer(model_name)
def encode_text(clip_model, text):
return clip_model.encode([text], convert_to_tensor=True, show_progress_bar=False)[0]
Below is a snippet of the data processing code encompassing the encoding and image processing functions. This is just a rough snippet - feel free to adjust it to your needs.
def create_latent_dataset_with_text_embeddings(dataset, vae_model_name, clip_model_name, output_folder, target_size=256, max_items=900000, aesthetic_threshold=5.5):
# Load the VAE model
vae = AutoencoderKL.from_pretrained(vae_model_name, torch_dtype=torch.float32)
vae.eval()
vae.to("cuda" if torch.cuda.is_available() else "cpu")
# Load the CLIP model for text embedding
clip_model = load_clip_text_encoder(clip_model_name)
# Create output folders and checkpoint file in Google Drive
latent_folder = os.path.join(output_folder, "latents")
os.makedirs(latent_folder, exist_ok=True)
checkpoint_file = os.path.join(output_folder, "checkpoint.txt")
# Load the last processed index
start_index = load_checkpoint(checkpoint_file)
print(f"Resuming from index {start_index}...")
# Process each image in the dataset
processed_count = 0
for idx, item in enumerate(tqdm(dataset, desc="Processing dataset")):
# Skip items before the last processed index
if idx < start_index:
continue
# Check if maximum items limit is reached
if processed_count >= max_items:
print(f"Reached maximum limit of {max_items} items. Stopping...")
break
# Extract relevant fields
url = item.get("url")
caption = item.get("caption", "")
# aesthetic_score = item.get("aesthetic_score", 0)
# # Skip items based on aesthetic_score
# if aesthetic_score and aesthetic_score < aesthetic_threshold:
# print(f"Skipping item due to low aesthetic_score ({aesthetic_score}): {url}")
# continue
if not url:
print(f"Skipping item with no URL: {item}")
continue
# Download the image
image = download_image(url)
if image is None:
continue # Skip the image if it failed to download
# Preprocess the image
processed_image = preprocess_image(image, target_size=target_size)
# Encode the latent representation
latent = encode_latent(vae, processed_image)
# Encode the caption text
text_embedding = encode_text(clip_model, caption)
# Save the latent and caption as a PyTorch object
latent_file = os.path.join(latent_folder, f"{str(idx).zfill(8)}.pt")
torch.save({
"latent": latent,
"caption": caption,
# "aesthetic_score": aesthetic_score,
"text_embedding": text_embedding.cpu() # Save tensor to CPU for portability
}, latent_file)
# Save checkpoint
save_checkpoint(checkpoint_file, idx)
# Increment processed count
processed_count += 1
print(f"Dataset created successfully with {processed_count} items!")
print(f"Latents saved in: {latent_folder}")
print(f"Checkpoint saved at index {start_index} in: {checkpoint_file}")
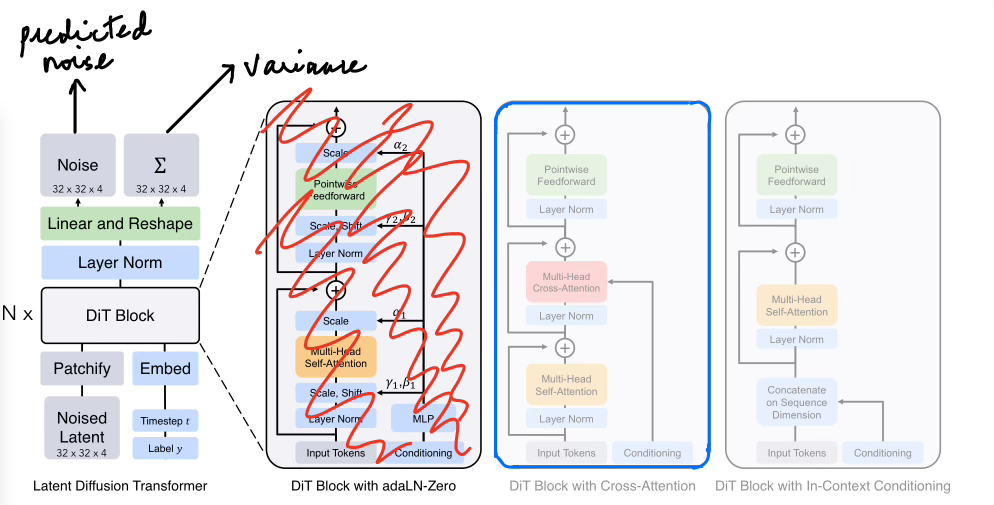
For our adaptation of the DiT, we will take the noisy latents we processed above to transform them into patches, then take it through the DiT attention block as outlined in blue and then perform processing to get the output denoised image. The image below should give you a good idea of the structure we’ll follow. The only difference is that the architecture below outputs predicted noise which would be removed from the noisy latent to give the denoised image. We, however, will just output the denoised latent directly.
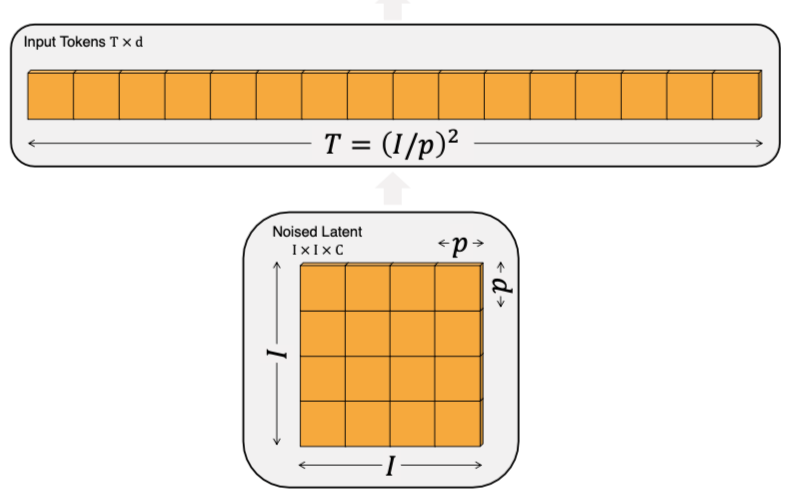
Patchification
Now coming to the meat of how to structure the DiT. Diffusion Transformers are heavily influenced by Vision Transformers where the image(after being decomposed into a latent using an autoencoder) is decomposed into a set of patches. After encoding, the latent is of shape 32 x 32 x 4 and to feed the latent to the model in a sequential manner, the image has to be divided into patches. The latent is passed through a convolutional layer to increase the channels and divide image into defined patch_size x patch_size(let it be 2 for this post - can be any divisible number) patches. The patches are then flattened and embedded to a pre-decided embed dimension(embed_dim).
Patchification is important for the following reasons:
- Computational Efficiency: Processing an entire image at once would be computationally expensive. Breaking it into patches allows the transformer to process smaller, manageable chunks of information.
- Local Feature Learning: Patches help preserve local spatial relationships while allowing the transformer to learn both local and global dependencies through self-attention.
- Memory Management: Working with patches instead of full images significantly reduces memory requirements, especially for high-resolution images.
patch_dim = self.patch_height * self.patch_width * self.image_channels
self.patchify_and_embed = nn.Sequential(
nn.Conv2d(self.image_channels, patch_dim, kernel_size=self.patch_height, stride=self.patch_width),
Rearrange("bs d h w -> bs (h w) d"),
nn.LayerNorm(patch_dim),
nn.Linear(patch_dim, self.embedding_dim),
nn.LayerNorm(self.embedding_dim),
)
So the size of the latent prior to patch convolution is (BATCH_SIZE, LATENT_HEIGHT, LATENT_WIDTH, LATENT CHANNELS) - (BATCH_SIZE, 32, 32, 4).
After dividing or convolving the image into patches, each latent is represented by shape of (BATCH_SIZE, NUMBER OF PATCHES, PATCH_DIM) and each patch is a convolution over a 2x2 space in the latent. For better representations each latent is embedded into a higher order embedding dimension(self.embedding_dim in the code) - let’s assume it to be 512 here. So the size becomes BATCH_SIZE, 256, 512). Now we have our normally oriented image broken into sequential patches.
You would have seen that we added a step of normalisation by doing nn.LayerNorm(self.embedding_dim). Layer normalization ensures that the inputs to each layer have a stable distribution by normalizing across the channel dimension, ensuring each feature map has zero mean and unit variance. This prevents issues such as internal covariate shift, improving convergence and overall stability. It is particularly important when embedding patches because the patch dimensions may vary slightly in scale or intensity. By normalizing layer-wise, the model can learn more effectively without being biased by outliers in certain patches.
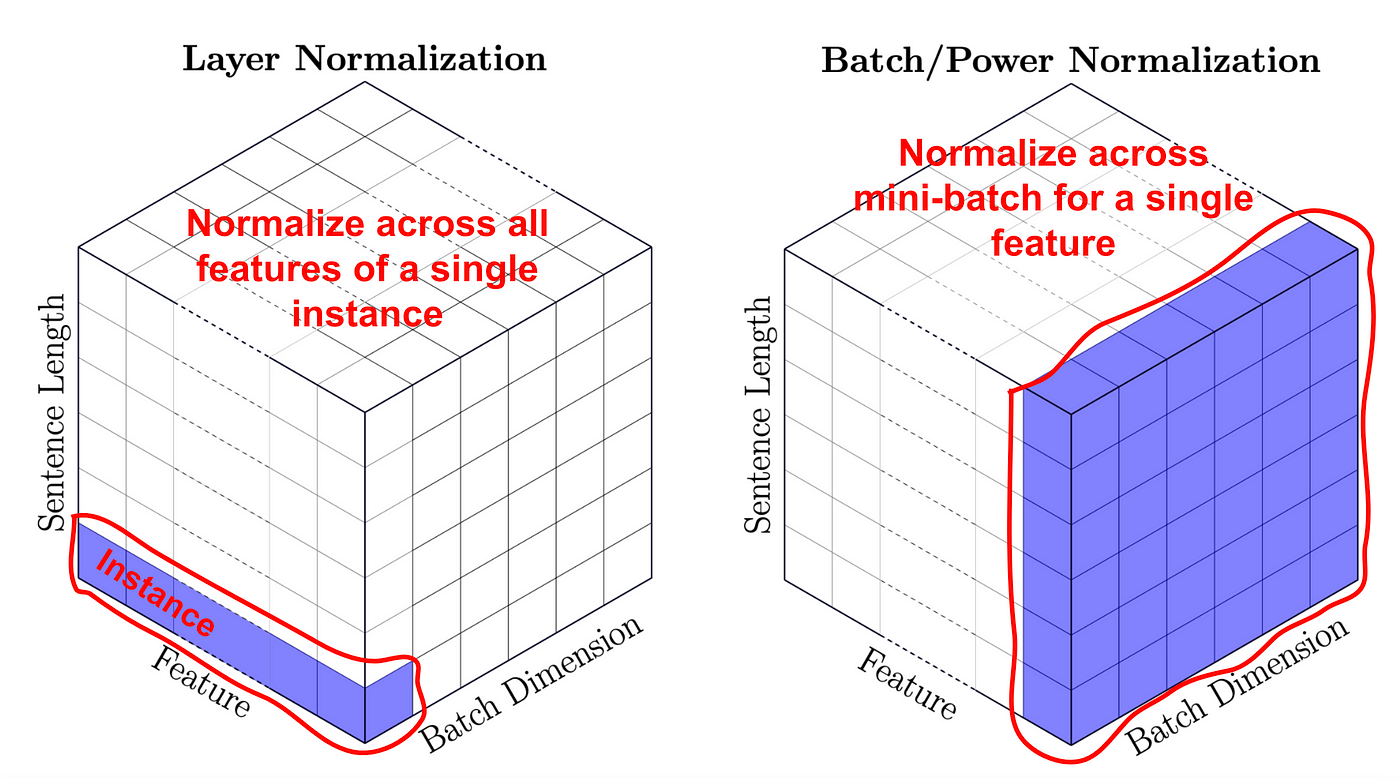
The image above shows how layer norm is done along the channel and ensures that each data point’s features are distributed normally versus batch normalization which isn’t effective in the case of diffusion processes since if two images have wildly different distributions, the batch statistics might not reflect any single data point well. This can cause distorted normalization for some data points, leading to unstable or poor learning.
Positional Embedding
But now you maybe wondering how the model understands an image’s orientation once we break it up into patches. Image pixels may not be sequential. This is where we add positional information of each patch through special embeddings. They make sure the spatial understanding of the image patches remains when passed through the transformer. The special embedding I referred to are absolute positional embeddings here.
Embeddings, in general, are dense vector representations of data, allowing models to translate discrete inputs (like words or image patches) into a continuous space where relationships can be learned. In the case of positional embeddings, these vectors provide information about the position of each patch in the image, ensuring that the model can maintain spatial coherence throughout processing. Think of positional embeddings almost as an address index where each positional embedding provides data of where a patch should be oriented in the overall image.
They will be defined as follows:
self.pos_embed = nn.Embedding(self.image_height * self.image_width // (self.patch_height * self.patch_width), self.embedding_dim)
self.register_buffer("precomputed_pos_enc", torch.arange(0, ((self.image_height * self.image_width) / (self.patch_width * self.patch_height))).long())
Here, self.pos_embed will have a shape of (NUMBER_OF_PATCHES, self.embedding_dim in the code) which will become (256, 512). The matching dimensionality helps in adding the “positional index” to the patch embedding.
Later, in the forward function, we add both the patchified image embedding representation and the positional embedding to get a combined representation. See here:
def forward(self, x):
x = self.patchify_and_embed(x)
pos_enc = self.precomputed_pos_enc[: x.size(1)].expand(x.size(0), -1)
x = x + self.pos_embed(pos_enc)
return x
So all put together, the patchify block would look something like this:
import torch
import torch.nn as nn
from einops.layers.torch import Rearrange
class PatchEmbedding(nn.Module):
def __init__(self, image_height, image_width, image_channels, patch_height, patch_width, embedding_dim):
super().__init__()
self.image_height = image_height
self.image_width = image_width
self.image_channels = image_channels
self.patch_height = patch_height
self.patch_width = patch_width
self.embedding_dim = embedding_dim
patch_dim = self.patch_height * self.patch_width * self.image_channels
self.patchify_and_embed = nn.Sequential(
nn.Conv2d(self.image_channels, patch_dim, kernel_size=self.patch_height, stride=self.patch_width),
Rearrange("bs d h w -> bs (h w) d"),
nn.LayerNorm(patch_dim),
nn.Linear(patch_dim, self.embedding_dim),
nn.LayerNorm(self.embedding_dim),
)
self.pos_embed = nn.Embedding(
self.image_height * self.image_width // (self.patch_height * self.patch_width), self.embedding_dim
)
self.register_buffer("precomputed_pos_enc", torch.arange(0, ((self.image_height * self.image_width) /
(self.patch_width * self.patch_height))).long())
def forward(self, x):
x = self.patchify_and_embed(x)
pos_enc = self.precomputed_pos_enc[: x.size(1)].expand(x.size(0), -1)
x = x + self.pos_embed(pos_enc)
return x
Noise Embeddings
One of the fundamental techniques in diffusion models is adding noise in a controlled manner and progressively removing it during training. This process helps the model focus on finer details when the noise level is low and on broader structures when the noise level is high. This noise is typically added using a predefined schedule, such as the cosine schedule, as shown below
def get_noise_schedule(t, start=0, end=1):
"""
Cosine noise schedule as proposed in Improved DDPM paper
"""
# Cosine schedule as proposed in https://arxiv.org/abs/2102.09672
s = 0.008 # Offset to prevent singularity
t = torch.as_tensor(t)
return torch.cos(((t / end + s) / (1 + s)) * math.pi * 0.5) ** 2
**steps before and after will be shown later**
t = torch.rand(batch_size, device=device)
# Get noise levels from cosine schedule
noise_level = get_noise_schedule(t)
signal_level = torch.sqrt(1 - noise_level) # Changed to sqrt for proper scaling
# Generate noise and mix with signal
noise = torch.randn_like(x, device=device)
x_noisy = (noise_level.view(-1, 1, 1, 1) * noise +
signal_level.view(-1, 1, 1, 1) * x)
x_noisy = x_noisy.float()
noise_level = noise_level.float()
In this schedule, the noise level gradually increases while the signal-to-noise ratio (the ratio between the original image content and the added noise) decreases. To represent this noise level in a way the model can effectively understand and leverage, it is converted into sinusoidal embeddings.
Sinusoidal embeddings are a way to encode the noise level into a higher-dimensional space, allowing the model to capture the temporal progression of noise across training steps. This encoding uses sinusoidal functions (sine and cosine waves) at varying frequencies, enabling the model to distinguish between different levels of noise.
Here’s how it works:
- Frequencies: A range of frequencies is chosen, spanning from low (slow changes) to high (rapid changes). These frequencies are logarithmically spaced to cover a broad spectrum.
- Embedding Values: The noise level is multiplied by these frequencies, resulting in sinusoidal patterns that vary in oscillation rates.
- Distinctiveness: Higher noise levels produce rapidly oscillating embeddings, while lower noise levels generate slower oscillations. This variation allows the model to understand "where it is" in the denoising process.
The reason we choose this range of frequencies from low to high is that it helps the model strongly understand the step it is present at. When multiplied with the noise value like below, a higher noise value will lead to rapid oscillation of consequential embedding position values while a low noise value will lead to slow and smooth oscillation of embedding position values. Looking at the graph below, they're sin graphs at different compositions of frequencies. Just imagine how rapidly the oscillations would go about when a high noise value is multiplied to an already high frequency graph. Conversely, how slow the oscillations would be when a low noise value is multiplied to a low frequency graph.
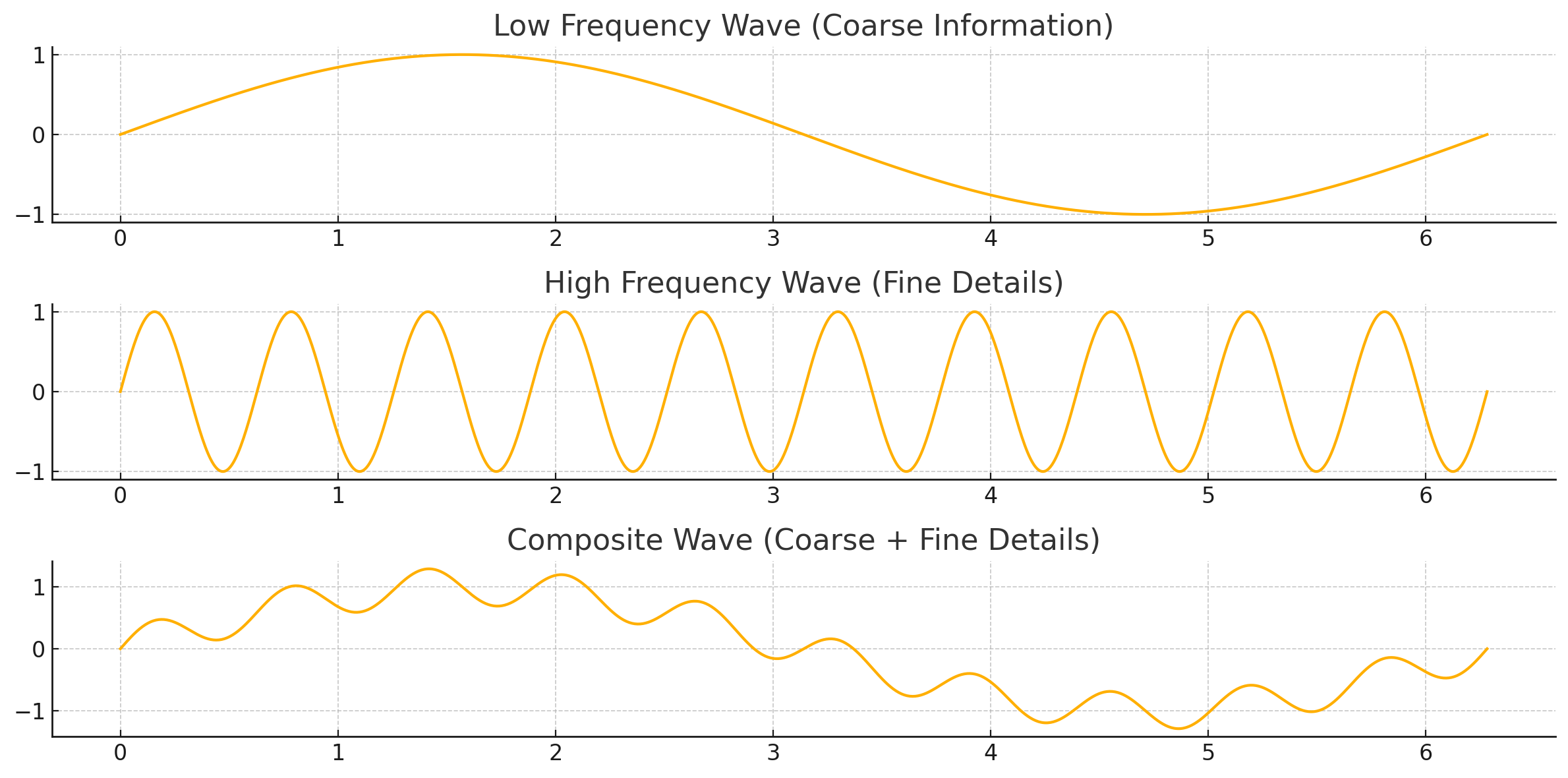
Frequency refers to how quick a signal changes over space(in an image). Low frequency means the signal changes slowly with large, smooth variations. High frequency means the signal changes rapidly with small, sharp variations. Thus, in images low-frequency components correspond to areas where pixel values change slowly across the image and high-frequency components are the ones that have sharp changes in pixel values. Thus, when the model observes rapidly oscillating noise embedding values(think of maybe quickly alternating positive/negative values), it directions itself to focus on finer sharper details while low frequency components(slowly changing values) help focusing on more broad changes.
import torch
import torch.nn as nn
import numpy as np
class SinusoidalEmbedding(nn.Module):
def __init__(self, embedding_dim, min_frequency=1.0, max_frequency=1000.0):
super().__init__()
# Create a range of frequencies spaced logarithmically between min and max frequency
# This ensures the model can capture both slow and fast variations in noise levels
freqs = torch.exp(torch.linspace(np.log(min_frequency), np.log(max_frequency), embedding_dim // 2))
# Convert frequencies to radians by multiplying by 2 * pi
# This allows the sinusoidal functions (sin/cos) to operate correctly over the full wave cycle
self.register_buffer("freqs", freqs * 2.0 * torch.pi)
def forward(self, x):
# Apply sine and cosine functions to the input x scaled by the frequencies
# This generates embeddings that oscillate at different rates
# Concatenate the sine and cosine embeddings along the last dimension
embeddings = torch.cat(
[torch.sin(self.freqs * x), torch.cos(self.freqs * x)], dim=-1
)
# Return the resulting high-dimensional sinusoidal embedding
return embeddings
Here, frequencies are generated logarithmically to span a broad spectrum, ensuring both slow and rapid variations are encoded. The sine and cosine components together ensure that each noise level has a unique, easily distinguishable embedding.
Self Attention
The most crucial component and backbone of the modern Transformer architecture are the attention layers. Attention layers help in two unique ways in DiTs. The first is for each patch of the latent image to understand/find relations with other patches and the second way would be to cross relate with the noise and text label embeddings. The former is known as self attention and the latter is known as cross-attention.
class SelfAttention(nn.Module):
def __init__(self, embed_dim, n_heads, dropout):
super().__init__()
self.embed_dim = embed_dim # 768
self.n_heads = n_heads # 12
self.head_dim = embed_dim // n_heads # 64
self.to_query = nn.Linear(embed_dim, embed_dim, bias=False)
self.to_key = nn.Linear(embed_dim, embed_dim, bias=False)
self.to_value = nn.Linear(embed_dim, embed_dim, bias=False)
self.to_dropout = nn.Dropout(dropout)
self.to_out = nn.Linear(embed_dim, embed_dim)
In attention mechanisms, a base embedding/vector is projected into three vectors - query, key and value vectors. Thus, each patch has its own query, key and value vectors. Each query vector of each patch is multiplied with the key vector of another patch. This score describes how well each patch’s query relates to each patch’s key(and inherently each patch). This is Self Attention.
# x: (B, 256, 768)
q, k, v = self.to_query(x), self.to_key(x), self.to_value(x) # (B, 256, 768)
q, k, v = map(
lambda t: t.view(t.shape[0], t.shape[1], self.n_heads, self.head_dim).transpose(1, 2),
(q, k, v)
) # q, k, v: (B, 12, 256, 64)
attention_weights = F.softmax(torch.matmul(q, k.transpose(-1, -2)) / (self.head_dim ** 0.5), dim=-1)
# k.transpose(-1, -2): (B, 12, 64, 256)
# attention_weights: (B, 12, 256, 256)
The attention scores are then put through a softmax function to get the weighted scores of relations between patches. Once the attention weights are computed by applying softmax, the next crucial step is to apply these weights to the value vectors. This ensures that patches that have stronger relationships (higher attention scores) contribute more to the final representation, while those with lower scores have a diminished influence.
In context of image reconstruction from noisy versions of them, here is an example of how it will work.
Imagine an image containing two distinct objects: a red dot and a blue dot, both partially obscured by noise. The image is divided into patches:
- Patch 1: Contains part of the red dot (but noisy)
- Patch 2: Background noise
- Patch 3: Contains part of the blue dot (also noisy)
- Patch 4: Contains another part of the red dot(less noisier than Patch 1)
At diffusion step t:
- Query (Q): Patch 1 asks, "Which other patches are similar to me?"
- Key (K): Patch 2, 3 and 4 respond with their representations
- Value (V): Each patch provides its latent information
The self-attention mechanism computes the similarity between (from the first red dot patch) and (from all patches). Since (another part of the red dot - patch 4) is more similar to Patch 1 than blue dot or noise, Patch 1 will attend more to Patch 4 and less to 2 or 3. This means that information from the red dot is reinforced while unrelated parts (like the blue dot) have less influence.
By performing a weighted sum of the value vectors using the attention weights, we allow the model to aggregate information from different parts of the latent image. This aggregation helps in reinforcing important related structures and patterns, while also preserving long-range dependencies, a characteristic strength of transformer architectures. This can be done in the following manner:
attention_weights = self.to_dropout(attention_weights) # (B, 12, 256, 256)
attention_output = torch.matmul(attention_weights, v) # (B, 12, 256, 64)
attention_output = attention_output.transpose(1, 2).reshape(x.shape[0], x.shape[1], self.embed_dim)
# attention_output: (B, 256, 12, 64) -> (B, 256, 768)
return self.to_out(attention_output) # (B, 256, 768)
Cross Attention
The cross attention mechanism is very similar to self-attention except that the query vector comes from one source of embeddings while the key and value vectors come from another source. This helps in creating cross-understanding between noise/text vectors and patch representations.
Imagine an image being generated from the prompt: "A red circle next to a blue square."
The image is divided into patches:
- Patch 1: Contains part of the red circle (but noisy)
- Patch 2: Background noise
- Patch 3: Contains part of the blue square (also noisy)
- Patch 4: Contains another part of the red circle (less noisy than Patch 1)
At diffusion step t:
- Query (Q): Patch 1 asks, "Which part of the text relates to me?"
- Key (K): The text embeddings (from the prompt) respond with representations of "red circle" and "blue square"
- Value (V): The text embeddings provide latent information about each described object
The cross-attention mechanism computes the similarity between Patch 1 (red circle part) and the text embeddings (red circle and blue square). Since the "red circle" embedding from the prompt closely aligns with Patch 1, Patch 1 will attend more to the "red circle" part of the text and less to the "blue square" or background noise.
This means information about the red circle is reinforced, guiding the diffusion model to refine the red circle in Patch 1, while unrelated descriptions (like the blue square) have less influence.
In contrast:
- Patch 3 (blue square) attends more to the "blue square" embedding from the text prompt
- Patch 2 (background noise) attends weakly to all text embeddings, as it lacks direct relevance to the described objects
During training, the model keeps refining its informational understanding of a caption embedding such as "red circle" or "blue square". So, over millions of images and pairing captions, the model starts developing latent knowledge of what labels or prompts refer to.
The code representation can be seen below - and the only difference you should see from the Self Attention mechanism is the source of the key and value vectors coming from a different source(y here which is the prompt + noise embedding).
class CrossAttention(nn.Module):
def __init__(self, embed_dim, n_heads, dropout):
super().__init__()
self.embed_dim = embed_dim # 768
self.n_heads = n_heads # 12
self.head_dim = embed_dim // n_heads # 64
self.to_query = nn.Linear(embed_dim, embed_dim, bias=False)
self.to_key = nn.Linear(embed_dim, embed_dim, bias=False)
self.to_value = nn.Linear(embed_dim, embed_dim, bias=False)
self.to_dropout = nn.Dropout(dropout)
self.to_out = nn.Linear(embed_dim, embed_dim)
def forward(self, x, y):
# x: (B, 256, 768), y: (B, T, 768)
q, k, v = self.to_query(x), self.to_key(y), self.to_value(y) # q: (B, 256, 768), k, v: (B, T, 768)
q, k, v = map(
lambda t: t.view(t.shape[0], t.shape[1], self.n_heads, self.head_dim).transpose(1, 2),
(q, k, v)
) # q: (B, 12, 256, 64), k, v: (B, 12, T, 64)
attention_weights = F.softmax(torch.matmul(q, k.transpose(-1, -2)) / (self.head_dim ** 0.5), dim=-1)
# k.transpose(-1, -2): (B, 12, 64, T)
# attention_weights: (B, 12, 256, T)
attention_weights = self.to_dropout(attention_weights) # (B, 12, 256, T)
attention_output = torch.matmul(attention_weights, v) # (B, 12, 256, 64)
attention_output = attention_output.transpose(1, 2).reshape(x.shape[0], x.shape[1], self.embed_dim)
# attention_output: (B, 256, 12, 64) -> (B, 256, 768)
return self.to_out(attention_output) # (B, 256, 768)
MLP Conv
In Diffusion Transformers, attention mechanisms form the backbone of the architecture, enabling patches to relate to each other and external embeddings (like noise or text). However, attention alone isn't sufficient to fully capture local patterns and complex hierarchical features within the latent representations. This is where MLPConv layers play a crucial role. Traditional MLPs, which process data globally, lack spatial understanding, while CNNs excel at local feature extraction but lack global context. MLPConv addresses these limitations by:
- Channel Expansion: Expanding the number of channels helps the model project latent features to a higher-dimensional space, allowing for richer feature representation.
- Depthwise Convolution (DWConv): The core of MLPConv involves depthwise convolutions that operate independently on each channel, capturing fine-grained spatial information.
class MLPConv(nn.Module):
def __init__(self, embed_dim, mlp_multiplier, dropout):
super().__init__()
self.conv = nn.Sequential(
nn.Conv2d(embed_dim, embed_dim * mlp_multiplier, kernel_size=1),
nn.Conv2d(embed_dim * mlp_multiplier, embed_dim * mlp_multiplier, kernel_size=3, padding=1, groups=embed_dim * mlp_multiplier),
nn.GELU(),
nn.Conv2d(embed_dim * mlp_multiplier, embed_dim, kernel_size=1),
nn.Dropout(dropout),
)
As seen above, the first layer in the Sequential self.conv object increases the channels to make the feature representation richer by increasing the channels to embed_dim * mlp_multiplier where mlp_multiplier is a pre-decided value(usually 4 or 8). We then use a depthwise convolution layer where we specify the number of groups being equal to the number of channels - all this does is ensures how many filters each channel will receive. This line nn.Conv2d(embed_dim * mlp_multiplier, embed_dim * mlp_multiplier, kernel_size=3, padding=1, groups=embed_dim * mlp_multiplier) specifically follows traditional transformer architectures by both expanding embed_dim to embed_dim with a multiplier like linear Feed-Forward networks and also let each position interact with its neighbours through a 3x3 convolution. By setting number of groups being equal to the number of channels, each channel gets its own filter, reducing the number of overall parameters.
This block is just utilised by writing the following forward function:
def forward(self, x):
h, w = int(x.size(1) ** 0.5), int(x.size(1) ** 0.5)
x = rearrange(x, "b (h w) c -> b c h w", h=h, w=w)
x = self.conv(x)
return rearrange(x, "b c h w -> b (h w) c")
Assembling all Blocks Together
Now let’s assimilate all of this together in the Denoiser class. First, we simply initialise the Denoiser class with necessary values -
import torch.nn as nn
from models.sinusoidal_embedding import SinusoidalEmbedding
from models.patch_embedding import PatchEmbedding
from models.attention import SelfAttention, CrossAttention
from models.mlp_conv import MLPConv
from einops import rearrange
import torch
class Denoiser(nn.Module):
def __init__(self, image_size, noise_embed_dims, patch_size, embed_dim, dropout, n_layers=10, text_emb_size=768, mlp_multiplier=8, n_channels=4):
super().__init__()
self.image_size = image_size
self.patch_size = patch_size
self.n_layers = n_layers
We then initialise and define all our previous classes to use.
self.noise_handling = nn.Sequential(
SinusoidalEmbedding(noise_embed_dims),
nn.Linear(noise_embed_dims, embed_dim),
nn.SiLU(),
nn.Linear(embed_dim, embed_dim)
)
self.patch_embedding_instance = PatchEmbedding(image_size, image_size, n_channels, patch_size, patch_size, embed_dim)
self.label_embedding = nn.Linear(text_emb_size, embed_dim)
We also create a module list for the patch, noise and label embeddings to go through where values are normalised after each major operation like Self Attention, Cross Attention and MLP Convolution(MLPConv).
# Repeated layers with normalization
self.layers = nn.ModuleList([
nn.ModuleDict({
"self_attn_norm": nn.LayerNorm(embed_dim),
"self_attention": SelfAttention(embed_dim, n_heads=12, dropout=dropout),
"cross_attn_norm": nn.LayerNorm(embed_dim),
"cross_attention": CrossAttention(embed_dim, n_heads=12, dropout=dropout),
"mlp_norm": nn.LayerNorm(embed_dim),
"mlp_conv": MLPConv(embed_dim, mlp_multiplier, dropout)
}) for _ in range(10)
])
To process the denoiser, we do the following:
patched_x = self.patch_embedding_instance(x)
label_embedding = self.label_embedding(text_label).unsqueeze(1)
noise_embedding = self.noise_handling(noise).unsqueeze(1)
noise_and_label_embedding = torch.cat([label_embedding, noise_embedding], dim=1)
Here, we take the noisy latent x and pass it through the instantiated patch_embedding_instance class to patchify the noisy latent into patches. At the same time, we pass the label_embedding through a label embedding layer that embeds the text embedding into the same embedding space/dimensionality as the patch embeddings. We “handle” the noise as defined earlier by giving it a sinusoidal representation and then projecting it into the same space as the patch embedding dimensionality. You’d also see a lot of different kinds of normalisation used in the model architecture like SiLU or GeLU - most of the times, they’re interchangeable - we just follow those norms because a certain previous implementation would’ve found some arbitrary benefit with a specific normalisation standard.
Following this, we concatenate the label and noise embeddings so that it is simpler to run cross attention on the noise and text combined at once than separately.
After this, the output of the previous operations is run through self.layers to perform attention and convolution mechanisms.
# Pass through repeated layers with normalization
out_x = patched_x
for layer in self.layers:
# Self attention with normalization
normed_x = layer["self_attn_norm"](out_x)
out_x = layer["self_attention"](normed_x) + out_x
# Cross attention with normalization
normed_x = layer["cross_attn_norm"](out_x)
out_x = layer["cross_attention"](normed_x, noise_and_label_embedding) + out_x
# MLP with normalization
normed_x = layer["mlp_norm"](out_x)
out_x = layer["mlp_conv"](normed_x) + out_x
At last, the image is run through a final layer of LayerNorm and a linear layer and re-arranged from patches to the shape of how the noisy latent looks.
out_x = self.final_norm(out_x)
out_x = self.out(out_x)
out = rearrange(out_x, 'b (h w) (c ps1 ps2) -> b c (h ps1) (w ps2)',
ps1=self.patch_size, ps2=self.patch_size,
h=int(self.image_size // self.patch_size),
w=int(self.image_size // self.patch_size))
return out
Training Loop: I'm going to show you a very basic loop without things like Exponential Moving Average and GPU optimisation settings. I will share links to these concepts or you can also look them up online.
import torch
import torch.nn.functional as F
from tqdm import tqdm
from models.denoiser import Denoiser
from dataset_loader import load_dataset
import os
def get_noise_schedule(t, start=0, end=1):
"""
Cosine noise schedule as proposed in Improved DDPM paper
"""
s = 0.008
t = torch.as_tensor(t)
return torch.cos(((t / end + s) / (1 + s)) * torch.pi * 0.5) ** 2
def train(train_loader, val_loader=None):
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# Model Initialization
model = Denoiser(
image_size=32,
noise_embed_dims=512,
patch_size=2,
embed_dim=512,
dropout=0.1,
n_layers=10
).to(device)
optimizer = torch.optim.AdamW(model.parameters(), lr=2e-4, weight_decay=0.03)
scheduler = torch.optim.lr_scheduler.OneCycleLR(
optimizer,
max_lr=8e-4,
epochs=50,
steps_per_epoch=len(train_loader),
pct_start=0.1,
div_factor=10
)
global_step = 0
# Training Loop
for epoch in range(1, 51):
model.train()
epoch_loss = 0
for x, y in tqdm(train_loader, desc=f"Epoch {epoch}"):
x, y = x.to(device), y.to(device)
x = x.float().mul_(0.18215) # Scale for VAE compatibility
batch_size = x.shape[0]
t = torch.rand(batch_size, device=device)
noise_level = get_noise_schedule(t)
noise = torch.randn_like(x)
x_noisy = noise_level.view(-1, 1, 1, 1) * noise + (1 - noise_level).sqrt().view(-1, 1, 1, 1) * x
optimizer.zero_grad()
pred = model(x_noisy, noise_level.view(-1, 1), y)
loss = F.mse_loss(pred, x)
loss.backward()
optimizer.step()
epoch_loss += loss.item()
global_step += 1
print(f"Epoch {epoch}: Loss = {epoch_loss / len(train_loader):.4f}")
scheduler.step()
print("Training complete!")
if __name__ == "__main__":
train_loader = load_dataset("./latents", batch_size=128)
train(train_loader)
Here are some notes and comments on the training loop procedure I used:
- I chose a OneCycleLR scheduler from the torch library. This scheduler gradually increases the learning rate to a peak (max_lr) before slowly decreasing it. This helps the model avoid any local maximas, a common occurrence if your training data is diverse in terms of variety of images as each different image can capture a different type of distribution. For example, my dataset composed of one set of images scraped from the net that covered photographs, diagrams, screenshots and another set that were midjourney generated images. Depending on how data is shuffled, models can learn one set of distributions really quickly and get stuck in a local maxima. This prompted the choice behind OneCycleLR.
- The data is scaled by a factor of 0.18215, which ensures compatibility with the latent space of the autoencoder. Specifically look here
x = x.float().mul_(0.18215) # Scale for VAE compatibility. VAEs, and other neural nets, perform better when the input data lies within a small, consistent range (e.g., -1 to 1 or 0 to 1) since scaled data helps in stable numerical operations/gradients and reduces the chance of exploding or vanishing gradients.
A Small Note on Attention
Attention mechanisms in transformers are built upon the concept of vector representations and their similarities in an n-dimensional space. Imagine you have two sets of vectors representing words or tokens. The similarity between these vectors can be calculated using the dot product, which reflects how closely related the tokens are in the embedding space. This is fundamental to understanding how attention assigns importance to different words in a sequence.
The seminal paper "Attention is All You Need" introduces three crucial vectors for each token: Query (Q), Key (K), and Value (V). This approach mirrors retrieval systems. Consider a database where keys represent topics and values hold information about those topics. To extract relevant information, a query is matched against the keys, and the most relevant values are retrieved. Similarly, in transformers, each token's query seeks to find the most relevant keys from other tokens, and their associated values contribute to the final output.
In practice, if you have two sentences, and you want to assess the relevance of a token from one sentence to all tokens in the second, the token's vector is transformed into a query. Every token in the second sentence generates its own key and value. The dot product between the query and each key results in similarity scores, which are passed through a softmax function to yield attention weights. These weights determine the contribution of each value to the final representation, guiding the model to focus on the most relevant parts of the input. By conceptualizing attention as a form of querying information, transformers efficiently capture dependencies between tokens, enabling state-of-the-art performance in tasks like translation, summarization, and more.
Attention mechanisms in transformers are built upon the concept of vector representations and their similarities in an n-dimensional space. The core computation can be broken down into three key steps:
1. First, we find similarity between Query and Keys. Since these are vectors, we compute dot products:
Q₁·[k₁₁, k₁₂, ..., k₁ₖ] = x₁, [v₁₁, v₁₂, ..., v₁ᵥ]
Q₁·[k₂₁, k₂₂, ..., k₂ₖ] = x₂, [v₂₁, v₂₂, ..., v₂ᵥ]
...
Q₁·[kₖ₁, kₖ₂, ..., kₖₖ] = xₖ, [vₖ₁, vₖ₂, ..., vₖᵥ]
2. We then normalize these similarity scores using softmax to get attention weights:
softmax(x) = softmax(Qᵢ·Kⱼ)
where i ∈ [1, 2, ..., n], j ∈ [1, 2, ..., z]
3. Finally, we compute the attention output by using these weights with the Values:
attention₁ = softmax(x)V = [y₁,y₂,...,yₖ] × [v₁₁ v₁₂ ... v₁ᵥ]
[v₂₁ v₂₂ ... v₂ᵥ]
[vₖ₁ vₖ₂ ... vₖᵥ] → shape(1,v)
This process mirrors information retrieval systems - the Query is like a search, Keys are like document titles, and Values are the document contents. The attention weights determine how much each Value contributes to the final representation.
In practice, this means that when processing text or image patches, each element can dynamically focus on other relevant elements, regardless of their position in the sequence. This is what makes transformers particularly powerful at capturing long-range dependencies and relationships in the input data.